ベクトルの直交分解からフーリエ変換のイメージを掴む

はじめに

フーリエ変換は、信号処理や物理学、工学など様々な分野で利用される強力な数学的手法です。しかし、具体的な原理については、なかなかとっつきづらい、、、という方が多いのではないでしょうか。

一方、「ベクトルの分解」はどうでしょう？ 高校数学や物理で、力を水平方向と垂直方向に分けたり、空間内の点の位置をx, y, z座標で表したりしましたよね。こちらは比較的イメージしやすいのではないでしょうか。

実は、この一見まったく異なるフーリエ変換とベクトルの直交分解の間には、下表のような深い類似性があり、 このアナロジー（類推）を使うと、フーリエ変換の本質がぐっと理解しやすくなります。

	ベクトルの直交分解	フーリエ級数展開（フーリエ変換のベース）
分解したい対象	ベクトル\(v\)	周期関数f(x)
何で分解するか	直交基底ベクトル\(e_n\)	直交基底関数 \(cos(n\omega x), sin(n\omega x)\)
分解の式	\(v = \sum_{n=1}^m a_n e_n\)	\(f(x)= \frac{a_0}{2} + \sum_{n=1}^\infty{}(a_n cos(n\omega x) + b_n sin(n\omega x))\)
係数の求め方	\(a_n = \frac{1}{e_n \cdot e_n}v \cdot e_n \quad (n=1,2…m) \)	\(a_n = \frac{2}{T} \int_0^T f(x)cos(n\omega x)dx,\quad (n = 0,1,2…) \) \(b_n = \frac{2}{T} \int_0^T f(x)sin(n\omega x)dx,\quad (n = 1,2…) \)

今回は、この興味深いつながりについて、紐解いていきましょう！

厳密な数学の話ではなく、あくまでフーリエ変換のイメージを掴むための説明です。

ベクトルの直交分解

単純な２次元ベクトルの直交分解について考えます。

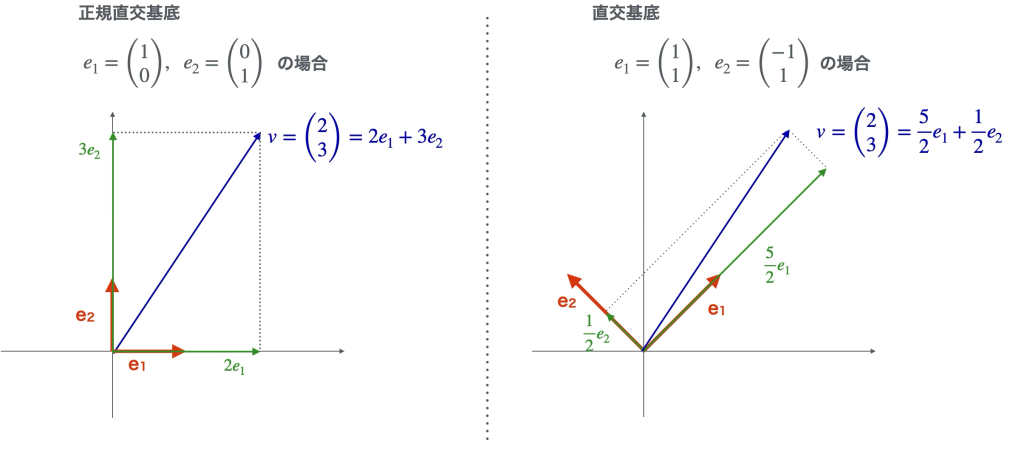
図の左側：正規直交基底による分解

まずは左側の図です。
ベクトル\(v = \begin{pmatrix} 2 \\ 3 \end{pmatrix}\) を、x軸方向の単位ベクトル\(e_{1}=\begin{pmatrix} 1\\ 0 \end{pmatrix}\)とy軸方向の単位ベクトル\(e_{2}=\begin{pmatrix} 0\\ 1 \end{pmatrix}\)で分解しています。

\[ v = \begin {pmatrix} 2 \\ 3 \end{pmatrix} = 2e_1+3e_2 \]

このとき、\(e_1\)と\(e_2\)のようなベクトルを正規直交基底と呼びます。

上記の例では直感的にこのように分解できることが分かったと思いますが、分解の仕組みをもう少し具体的に見てみましょう。
\(e_1, e_2\)は基底ベクトルであるため、すべてのベクトルはこれらの組み合わせで表現することができます。よって、任意のベクトルvは以下のように書けます。

\[ v = a_1 e_1 + a_2 e_2 \]

では、係数\(a_1, a_2\)はどのように求められるでしょうか？
両辺に\(e_1\)をかけてみます。

\[ v \cdot e_1 = a_1e_1 \cdot e_1 + a_2 e_2 \cdot e_1 \]

ここで、\(e_1\)の長さは1, \(e_1,e_2\)は直交していることから、\(a_1\)は以下となります。

\[a_1 = v \cdot e_1 \]

つまり\(e_1\)成分の大きさを知りたければ、元のベクトルと\(e_1\)との内積を計算すれば良い、ということになります。
同様に、\(a_2 = v \cdot e_2\) で求まります。

図の右側：直交基底による分解

次に図の右側を見てみましょう。同じベクトル\(v= \begin{pmatrix} 2 \\ 3 \end{pmatrix}\)を、今度は\(e_{1}=\begin{pmatrix} 1\\ 1 \end{pmatrix}\)と\(e_{2}=\begin{pmatrix} -1\\ 1 \end{pmatrix}\) という別の基底ベクトルで分解しています。

このとき、\(e_1, e_2\)は直交していますが、長さは1ではないため、”正規”ではない直交基底となります。
\(e_1, e_2\)は基底ベクトルのため、任意のベクトルvは同様に以下のように表せます。

\[ v = a_1 e_1 + a_2 e_2 \]

先ほど同様、両辺に\(e_1\)をかけてみます。

\[ v \cdot e_1 = a_1e_1 \cdot e_1 + a_2 e_2 \cdot e_1 \]

正規直交基底の場合は、\(e_1 \cdot e_1 = 1\)でしたが、今回は1にならないため、\(a_1\)は以下となります。

\[a_1 = \frac{1}{e_1\cdot e_1} v \cdot e_1 = \frac{1}{e_1^{2}} v \cdot e_1\]

同様に、\(e_2\)は以下となります。

\[a_2 = \frac{1}{e_2\cdot e_2} v \cdot e_2 = \frac{1}{e_2^{2}} v \cdot e_2\]

つまり、直交基底の場合は、内積を基底成分自身の内積（つまり長さの二乗）で割る必要があります。

実際に図の例で考えると、確かに以下のように求まります。

\[\begin{align}
&a_1 = \frac{1}{2} \begin{pmatrix} 2\\ 3 \end{pmatrix} \begin{pmatrix} 1\\ 1 \end{pmatrix} = \frac{5}{2} \\
&a_2 = \frac{1}{2} \begin{pmatrix} 2\\ 3 \end{pmatrix} \begin{pmatrix} -1\\ 1 \end{pmatrix} = \frac{1}{2}
\end{align}
\]

まとめると

正規直交基底も直交基底の一部であると考えれば、2次元ベクトルの直交分解は以下のようにまとめることができます。

\[\begin{align}
&v = \sum_{n=1}^2 a_n e_n \\
&a_n = \frac{1}{e_n \cdot e_n}v \cdot e_n \quad (n=1,2)
\end{align}
\]

さらにベクトルの次元を拡張し、m次元ベクトルの直交分解は以下のように記述することができます。

\[\begin{align}
&v = \sum_{n=1}^m a_n e_n \\
&a_n = \frac{1}{e_n \cdot e_n}v \cdot e_n \quad (n=1,2…m)
\end{align}
\]

フーリエ変換：関数を波で分解する

では本題のフーリエ変換です。
まず、フーリエ変換のベースとなるフーリエ級数展開から説明します。

フーリエ変換とフーリエ級数展開の関係性については以下記事で解説していますので、興味のある方は見てみてください。

フーリエ級数展開

比較表を再掲します。

	ベクトルの直交分解	フーリエ級数展開（フーリエ変換のベース）
分解したい対象	ベクトル\(v\)	周期関数f(x)
何で分解するか	直交基底ベクトル\(e_n\)	直交基底関数 \(cos(n\omega x), sin(n\omega x)\)
分解の式	\(v = \sum_{n=1}^m a_n e_n\)	\(f(x)= \frac{a_0}{2} + \sum_{n=1}^\infty{}(a_n cos(n\omega x) + b_n sin(n\omega x))\)
係数の求め方	\(a_n = \frac{1}{e_n \cdot e_n}v \cdot e_n \quad (n=1,2…m) \)	\(a_n = \frac{2}{T} \int_0^T f(x)cos(n\omega x)dx,\quad (n = 0,1,2…) \) \(b_n = \frac{2}{T} \int_0^T f(x)sin(n\omega x)dx,\quad (n = 1,2…) \)

フーリエ級数展開では周期関数f(x)を、直交基底ベクトルの代わりに、直交基底関数\(cos(n\omega x), sin(n\omega x)\)で分解します。
cos, sinが直交していることは、こちらのようなサイトを参照ください。

ベクトルのとき同様に、f(x)は以下のように表せます。
\[ f(x)= \frac{a_0}{2} + \sum_{n=1}^\infty{}(a_n cos(n\omega x) + b_n sin(n\omega x)) \]

係数\(a_n, b_n\)はベクトルのとき同様、元の関数f(x)と求めたい基底成分との内積を取って、その成分自身との内積で割ってあげればOKです。
よって、以下で求めることができます。

\[\begin{align}
&a_n = \frac{2}{T} \int_0^T f(x)cos(n\omega x)dx,\quad (n = 0,1,2…) \\
&b_n = \frac{2}{T} \int_0^T f(x)sin(n\omega x)dx,\quad (n = 1,2…)
\end{align}
\]

関数の内積＝積の積分です

このとき、cos, sinではその成分自身との内積は\(\frac{T}{2}\)となるため、その逆数の\(\frac{2}{T}\)が先頭にきています。

フーリエ変換

フーリエ変換は、フーリエ級数展開に以下処理をしたものになります。

• オイラーの公式を用いて、式をシンプルに
• 対象関数を周期関数から非周期関数に拡大

その結果、非周期関数f(x)は以下のように表すことができ、

\[f(x) = \frac{1}{2\pi} \int_{-\infty}^{\infty} F(\omega)e^{i\omega x}d\omega\]

係数\(F(\omega)\)は以下となります。これがいわゆるフーリエ変換の式です。

\[F(\omega) = \int_{-\infty}^{\infty}f(x)e^{-i\omega x}dx \]

結局この式の本質は、元の関数と求めたい基底成分の内積を取ることで、その基底成分の大きさを求めているに過ぎません。

まとめ

まとめると、フーリエ変換の本質は「関数を直交基底関数（複素指数関数やサイン・コサイン波）に分解して、その各成分の量を係数として求める」ことにあり、これはまさにベクトルの直交分解の考え方そのものです。

このように、ベクトルの直交分解（特に長さの正規化を含む考え方）のアナロジーを用いることで、フーリエ変換やフーリエ級数展開の数式の意味がより深く、直感的に理解できるのではないでしょうか。

一見複雑に見える操作も、基本的な原理は共通していることが多いです。今回の記事が、皆さんのフーリエ変換への理解を助け、数学や物理の世界の面白さを感じるきっかけになれば幸いです。