一次遅れ系を微分方程式から捉える

2025年7月26日

一次遅れ系とは、ある物理変数y（温度、電圧等）の時間変化が、次の一階線形微分方程式に従う系のことです。

$$\frac{dy}{dt} = -ay + b(t)\quad (a>0)\tag{1}$$

本記事ではこの式の物理的意味について、説明します。

一般的な解釈

(1)式は次のように変形できます。

$$\frac{dy}{dt} = a(\frac{b(t)}{a} – y) \tag{2} $$

下図に示すように、yは単調増加もしくは単調減少関数で、かつ$\frac{dy}{dt} = 0$となるのは、$y = \frac{b(t)}{a}$であるため、この$y = \frac{b(t)}{a}$が最終値（目標値）を意味します。

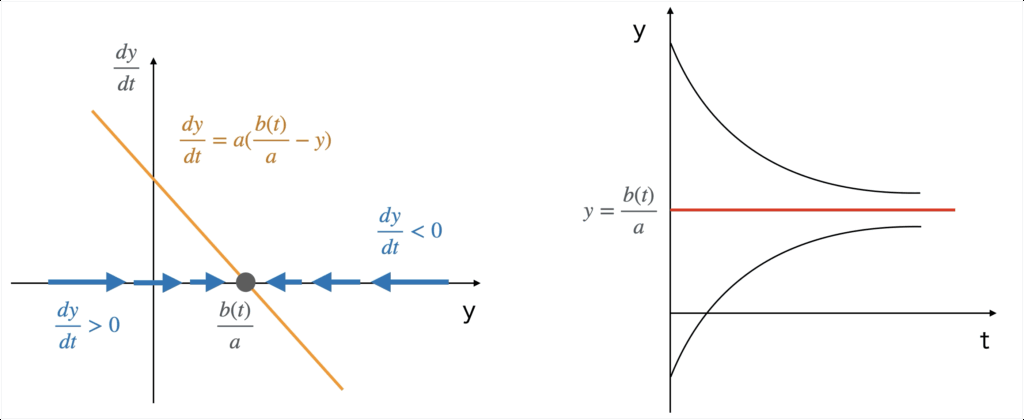
よって、(2)式から目標値と現在値の差分が大きいほど、速く変化するという特性がわかります。

ここで、次のように変数を置き換えます。

$$\tau = \frac{1}{a} \\
Ku(t) = \frac{b(t)}{a}
$$

$\tau$：時定数 (s)
Ku(t)：目標値
u(t)：入力値
K：目標値を入力値の何倍にするか

すると、(2)式は次のようになります。

$$\tau\frac{dy}{dt} = Ku(t) – y \tag{3}$$

数学的な一階微分方程式から、一般的によく見る物理の一次遅れの式に変形できました。

もう一つの解釈

目標値と現在値の差分で表すのが一般的な解釈ですが、駆動力 – 抵抗 という解釈も可能です。

「電車に乗り込む速さ」を例に説明します。

混んだ電車に毎日乗って通勤する人にとって、一次遅れ現象は身近なものでしょう。この例では、電車のドアーが‘抵抗’で車室が‘容量’になる一次遅れ要素と考えられます。

ホームに待っている人々の力で、前に待っている人々はかなりの力で車内に押し込まれ、勢いよく詰め込まれ始めます。しかし、乗客が入れば入るほど後ろの乗客に背圧をおよぼすので、乗り込む速度が遅くなります。

乗車人数が増えるにつれて乗車速度が下がるので、この現象を微分方程式で表すと、次のようになります。

$$\frac{dN}{dt} = f – kN $$

N: 乗車人数、f：抵抗がない場合の乗車速度（人/s）、k：正の定数

これは駆動力 – 抵抗の形で表現される一次遅れの式になります。

また、先ほど示したようにこの式を目標値 – 現在値の形に変形することも可能です。

$$\frac{dN}{dt} = f – kN = k(\frac{f}{k} – N) = \frac{1}{\tau}(a – N)$$

$\tau$：時定数、a：最大乗車人数